Exercises for Question Type 2: Finding the area of a closed region within a Voronoi Diagram

Question 1

Skill question

Seven sites are at $(1, 1)$ , $(5, 2)$ , $(3, 6)$ , $(0, 4)$ , $(- 1, 1)$ , $(3, 0)$ and the central site at $(2, 2)$ . Compute the area of the Voronoi cell around $(2, 2)$ .

[7]

Question 2

Skill question

Six sites lie at $(2, 1)$ , $(5, 1)$ , $(4, 4)$ , $(1, 3)$ , $(0, 1)$ and the center site at $(2, 2)$ . Determine the area of the Voronoi cell surrounding the point $(2, 2)$ .

[5]

Question 3

Skill question

The problem involves calculating the area of a Voronoi cell for a center site surrounded by six other sites forming a rectangular pattern. The sites are $(0, 0), (3, 0), (6, 0), (0, 4), (3, 4), (6, 4)$ and $(3, 2)$ .

A Voronoi diagram is defined by seven sites in the Cartesian plane. Six of these sites are located at the corners and midpoints of the longer edges of a rectangle: $(0, 0)$ , $(3, 0)$ , $(6, 0)$ , $(0, 4)$ , $(3, 4)$ , and $(6, 4)$ . The seventh site is located at the center of the rectangle, $(3, 2)$ .

Calculate the area of the Voronoi cell for the site at $(3, 2)$ .

[6]

Question 4

Skill question

Six points lie at the vertices of a regular hexagon of circumradius $3$ centered at the origin. Find the area of the Voronoi cell of the center.

[4]

Question 5

Skill question

Eight sites are located at $(2, 2)$ , $(- 2, 2)$ , $(- 2, - 2)$ , $(2, - 2)$ , $(3, 0)$ , $(0, 3)$ , $(- 3, 0)$ , and $(0, - 3)$ . A ninth site is located at the origin $(0, 0)$ .

Find the area of the Voronoi cell for the site at the origin.

[6]

Question 6

Skill question

Twelve points lie equally spaced on a circle of radius $6$ centred at the origin. Find the area of the Voronoi cell of the origin.

[4]

Question 7

Skill question

Eight points lie on a circle of radius $4$ equally spaced around the origin. Compute the area of the Voronoi cell of the origin.

[4]

Question 8

Skill question

Ten points lie on a circle of radius $5$ equally spaced around the origin. Find the area of the Voronoi cell of the origin.

[5]

Question 9

Skill question

A set of five points is given in the Cartesian plane as shown in the diagram below.

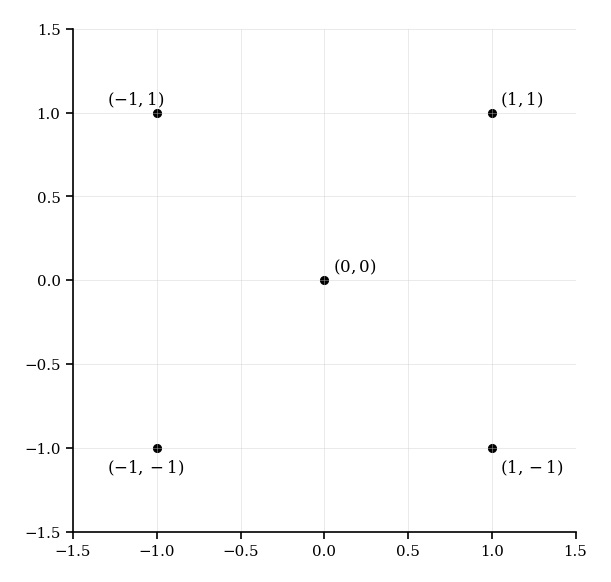
Given the five points at $(0, 0)$ , $(1, 1)$ , $(- 1, 1)$ , $(- 1, - 1)$ and $(1, - 1)$ , find the area of the Voronoi cell corresponding to the point $(0, 0)$ .

[6]

Question 10

Skill question

Five sites are located in a plane. Four of the sites are at $A (0, 0)$ , $B (6, 0)$ , $C (3, 5)$ , and $D (0, 5)$ . The fifth site, $P$ , is located at $(2, 2)$ . Determine the area of the Voronoi cell containing the site $P$ .

[6]

Question 11

Skill question

Five sites are at $(1, 0)$ , $(4, 0)$ , $(4, 3)$ , $(1, 3)$ and the center site at $(2.5, 1.5)$ . Find the area of the Voronoi cell around $(2.5, 1.5)$ .

[3]

IB Mathematics Applications & Interpretation Question Type 2: Finding the Area of a Closed Region Within a Voronoi Diagram Exercises