The Arrhenius Equation: Understanding Temperature's Role in Reaction Rates
- In the previous article, we covered rate constant, considering it in relation to Arrhenius equations.
- In this article, let's explore Arrhenius equation separately in more detail.
The Arrhenius Equation and Its Components
The Arrhenius equation is expressed as:
$$
k = A e^{-\frac{E_a}{RT}}
$$
where:
- $k$: The rate constant, which determines the speed of the reaction.
- $A$: The Arrhenius factor(or frequency factor), representing the frequency of collisions with the correct orientation for a reaction to occur.
- $E_a$: The activation energy, the energy barrier that must be overcome for a reaction to proceed (measured in joules per mole, $\text{J mol}^{-1}$).
- $R$: The gas constant, $8.31 \, \text{J mol}^{-1}\ \text{K}^{-1}$.
- $T$: The absolute temperature in kelvin (K).
- $e$: The base of natural logarithms ($e \approx 2.718$).
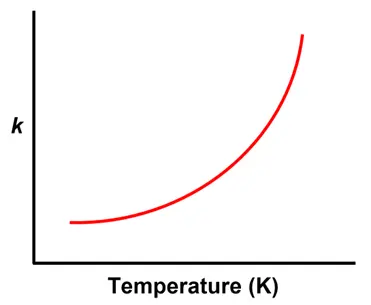
This equation tells us two key things:
- As temperature increases ($T$), the term $-\frac{E_a}{RT}$ becomes less negative.
- This means $e^{-\frac{E_a}{RT}}$ increases, leading to a larger $k$, and thus a faster reaction.
- A higher activation energy ($E_a$) reduces $k$.
- Reactions with large activation energies are slower because fewer particles have enough energy to overcome the barrier.
The exponential term, $e^{-\frac{E_a}{RT}}$, represents the fraction of particles with enough energy to overcome the activation energy barrier at a given temperature.
The Linear Form of the Arrhenius Equation
- The Arrhenius equation can also be expressed in a linear form for easier analysis: $$
\ln k = \ln A - \frac{E_a}{RT}
$$ - This equation is in the form of a straight-line equation: $y = mx + c$, where:
- $y = \ln k$
- $x = \frac{1}{T}$
- The slope ($m$) is $-\frac{E_a}{R}$.
- The y-intercept ($c$) is $\ln A$.
- By plotting $\ln k$ against $\frac{1}{T}$, you can determine the activation energy ($E_a$) and the frequency factor ($A$) from the graph:
- The slope of the line gives $-\frac{E_a}{R}$. Rearranging, $E_a = -\text{slope} \times R$.
- The y-intercept gives $\ln A$, so $A = e^{\text{y-intercept}}$.
Determining Activation Energy
Consider a reaction with the following data:
| Temperature (T) / K | Rate constant (k) / $\text{s}^{-1}$ |
|---|---|
| 300 | 2.5 |
| 350 | 6.8 |
Convert the data to $\ln k$ and $\frac{1}{T}$:- For $T = 300$: $\ln k = \ln(2.5) = 0.916$, $\frac{1}{T} = \frac{1}{300} = 0.00333$.
- For $T = 350$: $\ln k = \ln(6.8) = 1.918$, $\frac{1}{T} = \frac{1}{350} = 0.00286$.
- Plot $\ln k$ against $\frac{1}{T}$ to obtain a straight line.
- The slope of the line is $-\frac{E_a}{R}$.
- Calculate $E_a$:
- Slope = $\frac{\ln k_2 - \ln k_1}{\frac{1}{T_2} - \frac{1}{T_1}} = \frac{1.918 - 0.916}{0.00286 - 0.00333} = -2100 \, \text{K}$ $$E_a = -\text{slope} \times R$$ $$= -(-2100) \times 8.31 = 17451 \, \text{J mol}^{-1} = 17.45 \, \text{kJ mol}^{-1}$.
Why Does Temperature Affect Reaction Rates?
- To understand why temperature has such a significant impact on reaction rates, we turn to the Maxwell-Boltzmann distribution.
- This distribution describes the spread of kinetic energies among particles in a sample.
Key Points:
- At any temperature, most particles have a kinetic energy close to the average, but some have much higher energies.
- As temperature increases:
- The average kinetic energy of particles increases.
- The distribution curve flattens and shifts to the right, increasing the number of particles with energy greater than $E_a$.
This explains the exponential relationship between temperature and the rate constant in the Arrhenius equation.
Determining Activation Energy Experimentally
The activation energy of a reaction can be determined by measuring the rate constant ($k$) at different temperatures and using the linear form of the Arrhenius equation.
Steps:
- Conduct the reaction at several temperatures and determine $k$ at each temperature.
- Calculate $\ln k$ and $\frac{1}{T}$ for each data point.
- Plot $\ln k$ against $\frac{1}{T}$.
- Determine the slope ($-\frac{E_a}{R}$) and calculate $E_a$.
When performing experiments, ensure that all other variables (e.g., concentration, pressure) remain constant to isolate the effect of temperature.
- What happens to the rate constant ($k$) if the temperature is doubled?
- How would you determine the activation energy of a reaction using experimental data?
- Why does a higher activation energy result in a slower reaction?