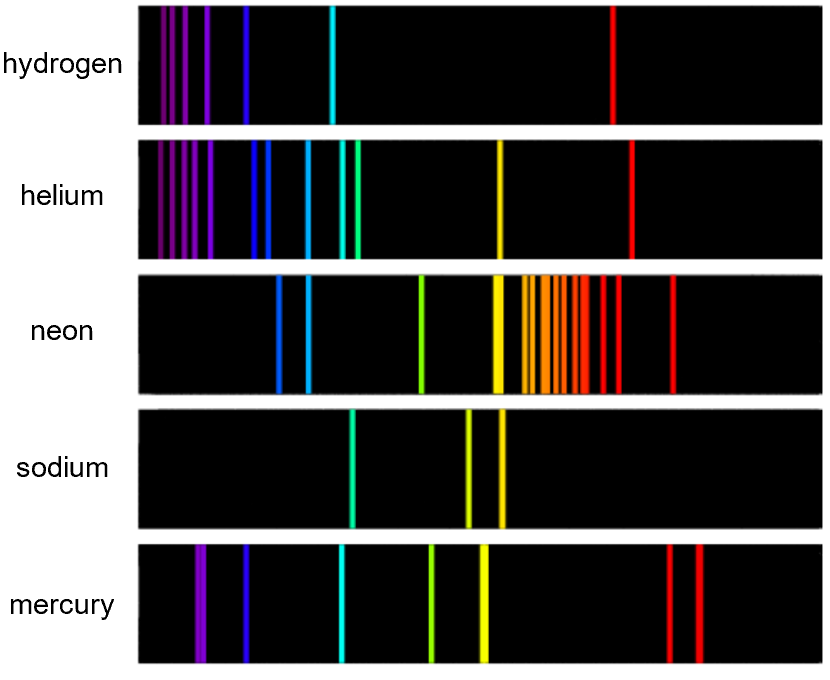
Emission and Absorption Spectra, Photon Energy, and Spectral Applications
- When standing in a pitch-dark room, you hold a glowing tube of gas in one hand and a prism in the other.
- As you shine the gas's light through the prism, a series of colorful lines appears on the wall.
- These lines aren't random, they represent the unique "fingerprint" of the gas.
What you’re seeing is an emission spectrum, which shows how energy exists in discrete levels in an atom
Light Emission: Electrons Transitioning to Lower Energy Levels
- Think about a hydrogen atom: it consists of a single electron orbiting a positively charged nucleus (a proton).
- Within the atom, the electron can only exist in specific energy levels, which are quantized.
- This means the electron cannot possess an arbitrary amount of energy, it must "choose" from a discrete set of allowed energy levels.
How Does Light Emerge?
When an electron transitions from a higher energy level to a lower one, it releases energy in the form of light.
This light is emitted as a photon.
Photon
A photon is a tiny particle that comprises waves of electromagnetic radiation.
- Photon's energy determined by the equation: $$E = hf$$ where:
- $E$ is the energy of the photon,
- $h = 6.63 \times 10^{-34} \, \text{J·s}$ is Planck’s constant,
- $f$ is the frequency of the emitted light.
- The frequency $f$ determines the color of the light.
- Since the energy levels in an atom are fixed, the emitted light has specific, predictable wavelengths.
- When passed through a prism or diffraction grating, this light separates into distinct lines, forming the emission spectrum.
Emission spectrum
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted due to an atom or molecule transitioning from a high energy state to a lower energy state.
- Consider an electron in a hydrogen atom transitioning from the $n = 3$ energy level $-1.51 \, \text{eV})$ to the $n = 2$ energy level $-3.40 \, \text{eV}$.
- The energy of the emitted photon is: $$\Delta E = E_{n=3} - E_{n=2} = -1.51 \, \text{eV} - (-3.40 \, \text{eV}) = 1.89 \, \text{eV}$$
- Convert this energy to joules $1 \, \text{eV} = 1.6 \times 10^{-19} \, \text{J})): $$\Delta E = 1.89 \times 1.6 \times 10^{-19} = 3.024 \times 10^{-19} \, \text{J}$$
- The wavelength (\lambda) of the emitted photon is calculated using: $$\lambda = \frac{hc}{\Delta E} = \frac{6.63 \times 10^{-34} \times 3.0 \times 10^8}{3.024 \times 10^{-19}} = 6.58 \times 10^{-7} \, \text{m}$$
- This wavelength corresponds to red light, visible in the hydrogen emission spectrum.
Light Absorption: Electrons Transitioning to Higher Energy Levels
- Now, consider shining white light (which contains all colors) through a gas.
- As the light passes through, certain wavelengths are absorbed by the gas, leaving dark lines in the transmitted light.
- These dark lines form the absorption spectrum.
Absorption spectrum
Absorption spectrum is the range of frequencies of electromagnetic radiation readily absorbed by a substance by virtue of its chemical composition.