Exercises for Question Type 2: Finding minimum spanning trees by applying Kruskal's algorithm

Question 1

Given the weighted undirected graph with vertices A, B, C, D and edges with weights: (A, B) = 1, (A, C) = 3, (A, D) = 4, (B, C) = 2, (C, D) = 5 . Use Kruskal's algorithm to find the minimum spanning tree (MST). List the edges in the MST and its total weight.

[5]

Question 2

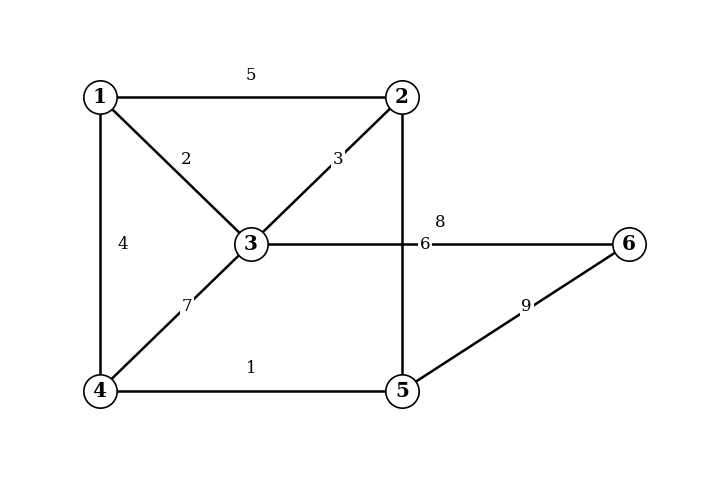
The following weighted graph has 6 vertices, labeled 1-6. The weights of the edges are: (4, 5) = 1 (1, 3) = 2 (2, 3) = 3 (1, 4) = 4 (1, 2) = 5 (2, 5) = 6 (3, 4) = 7 (3, 6) = 8 (5, 6) = 9

Apply Kruskal's algorithm to find the minimum spanning tree (MST) for the graph. State the edges in the order they are considered, indicating whether each is included or rejected, and find the total weight of the MST.

[5]

Question 3

A complete graph has vertices A, B, C, D, E and edge weights as follows: (A, B) = 2 (A, C) = 9 (A, D) = 3 (A, E) = 6 (B, C) = 1 (B, D) = 7 (B, E) = 8 (C, D) = 4 (C, E) = 5 (D, E) = 10 Find the minimum spanning tree (MST) using Kruskal's algorithm and state its total weight.

[5]

Question 4

Discrete mathematics: Graph theory

The vertices 1, 2, 3, 4, 5, 6, 7 of a graph are connected by edges with the following weights: (1, 2) = 4 (1, 3) = 2 (2, 3) = 1 (2, 4) = 7 (3, 5) = 5 (4, 5) = 3 (4, 6) = 6 (5, 7) = 8 (6, 7) = 9 Find the minimum spanning tree (MST) for this graph using Kruskal's algorithm and state its total weight.

[5]

Question 5

A weighted graph has vertices A, B, C, D, E . The weights of the edges are given in the following table: Edge Weight (A, B) 3 (A, C) 2 (A, D) 4 (B, C) 1 (B, E) 5 (C, D) 6 (C, E) 7 (D, E) 8 Apply Kruskal's algorithm to determine the minimum spanning tree (MST) and its total weight. Show your working clearly.

[6]

Question 6

The question tests the application of Kruskal's algorithm to find the Minimum Spanning Tree (MST) of a given weighted graph. Students must demonstrate sorting edges by weight and correctly selecting edges while avoiding cycles.

A weighted graph has vertices P, Q, R, S, T, U, V and the following edges with their respective weights: (P, Q) = 3, (P, R) = 2, (Q, R) = 1, (Q, S) = 4, (R, T) = 5, (S, T) = 6, (S, U) = 7, (T, V) = 8, (U, V) = 9 Use Kruskal's algorithm to determine the edges in the minimum spanning tree (MST) and calculate its total weight.

[4]

Question 7

A graph with vertices {A, B, C, D, E, F, G} has the following edges and weights: (A, B) = 2 (A, C) = 4 (B, C) = 1 (B, D) = 5 (C, E) = 3 (D, E) = 6 (D, F) = 7 (E, G) = 8 (F, G) = 9 Find the minimum spanning tree (MST) using Kruskal's algorithm and state its total weight.

[6]

Question 8

Consider the graph with vertices {1, 2, 3, 4, 5} and edge weights: (1, 2) = 10, (1, 3) = 8, (1, 4) = 5, (2, 3) = 7, (2, 5) = 6, (3, 4) = 9, (4, 5) = 2, (3, 5) = 3 . Use Kruskal's algorithm to find the minimum spanning tree and its total weight.

[4]

Question 9

A graph on vertices A, B, C, D, E, F has edges and weights: (A, B) = 2, (A, C) = 5, (B, C) = 1, (B, D) = 4, (C, E) = 3, (D, E) = 6, (D, F) = 7, (E, F) = 8 . Use Kruskal's algorithm to derive the Minimum Spanning Tree (MST) and its overall weight.

[6]

Question 10

A graph has vertices A, B, C, D, E and the following weighted edges: (A, B) = 2, (A, C) = 4, (B, D) = 3, (C, D) = 5, (B, C) = 1, (D, E) = 6, (C, E) = 7 Apply Kruskal's algorithm to determine the minimum spanning tree (MST) for this graph and compute its total weight. Show the steps of the algorithm, including which edges are selected or rejected.

[5]

Question 11

Consider the graph with vertices V = {1, 2, 3, 4, 5, 6} and weighted edges E : (1, 2) = 3 (1, 3) = 1 (2, 3) = 7 (2, 4) = 5 (3, 5) = 4 (4, 5) = 2 (4, 6) = 6 (5, 6) = 8 Use Kruskal's algorithm to find the minimum spanning tree (MST) of the graph and state its total weight.

[5]

IB Mathematics Applications & Interpretation Question Type 2: Finding Minimum Spanning Trees by Applying Kruskal's Algorithm Exercises