IB Mathematics Applications & Interpretation Question Type 1: Construction Transition Matrices from Diagrams or Context Descriptions Exercises

Given the transition matrix $$P=\left(\begin{array}{ccc}0.5& 0.3& 0.2\\ 0.2& 0.5& 0.3\\ 0.1& 0.4& 0.5\end{array}\right),$$ calculate the two-step transition probability from state 1 to state 3 by computing $(P^2{)}_{13}$ and interpret its meaning.

What is the probability that a customer moves from shop B to shop D in one step? Interpret your answer in context.

Consider the following state transition diagram for a Markov chain with states $X$, $Y$, and $Z$:

Draw on this

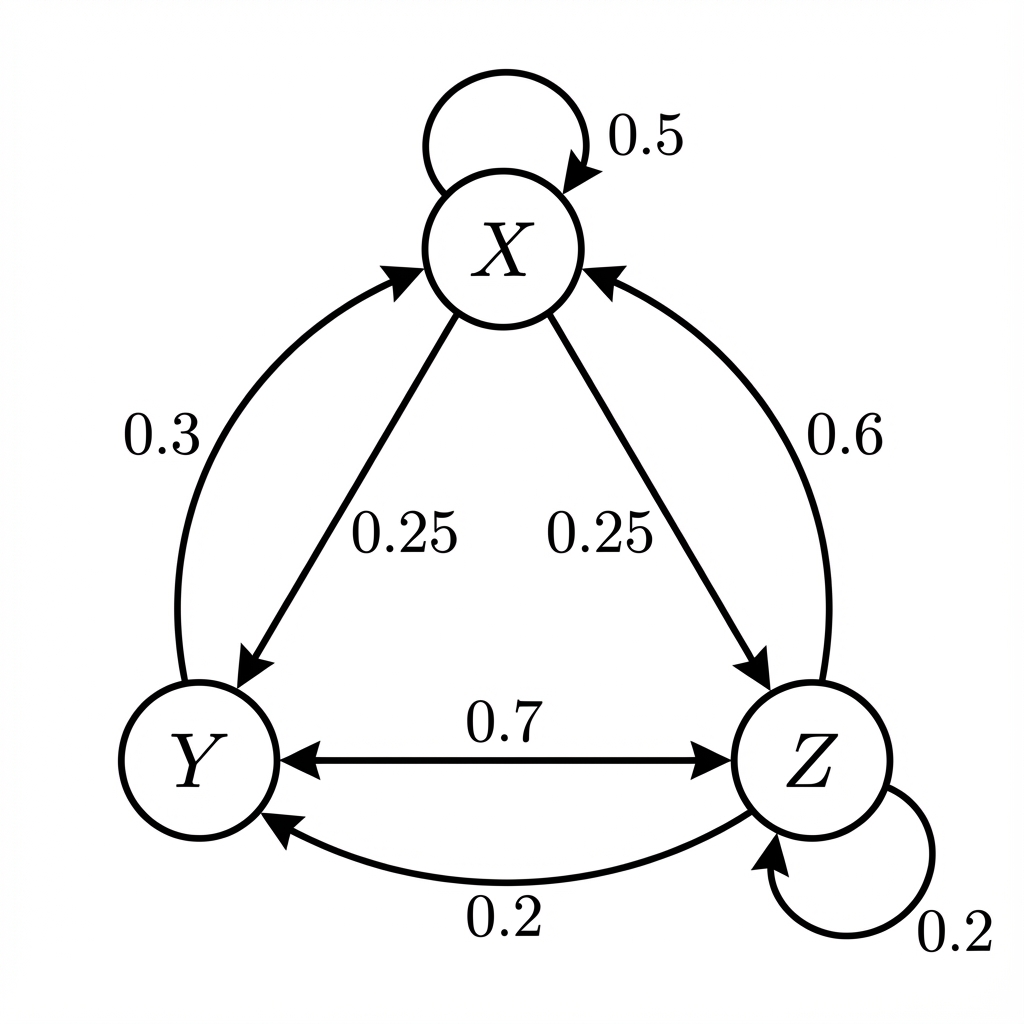
(a) Construct the transition matrix, $\mathbf{P}$, for the states $X,Y,$ and $Z$ in that order.

(b) Interpret the entry $p_{23}$ in the context of the diagram.

Construct the transition matrix for a Markov chain with states Sunny ($S$) and Rainy ($R$), given that if it is Sunny today it stays Sunny tomorrow with probability $0.8$ and becomes Rainy with probability $0.2$, and if it is Rainy today it becomes Sunny with probability $0.5$ and stays Rainy with probability $0.5$.

Interpret the third row of the transition matrix $P$:

$$P=\left(\begin{array}{ccc}0.2& 0.5& 0.3\\ 0.1& 0.7& 0.2\\ 0.3& 0.2& 0.5\end{array}\right)$$

Explain what the entries in row 3 represent.

Given the transition matrix

$$P=\left(\begin{array}{cc}0.6& 0.4\\ 0.3& 0.7\end{array}\right),$$

interpret the entry $p_{12}=0.4$.

A machine can be either On ($O$) or Off ($F$). If it is On, it stays On with probability $0.9$ and switches Off with probability $0.1$. If it is Off, it stays Off with probability $0.7$ and switches On with probability $0.3$.

Write the transition matrix with states in the order $(O,F)$.

In a cohort of students, transitions each year between courses Mathematics ($M$), Physics ($P$), and Chemistry ($C$) occur as follows:

• Of those in $M$: 50 stay in $M$, 30 move to $P$, and 20 move to $C$.
• Of those in $P$: 20 move to $M$, 60 stay in $P$, and 20 move to $C$.
• Of those in $C$: 10 move to $M$, 30 move to $P$, and 60 stay in $C$.

Construct the transition matrix $\mathbf{P}$ for this system, with states ordered ($M,P,C$).

A gambler’s fortune has three levels: Low ($L$), Medium ($M$), and High ($H$).

If at $L$, he stays at $L$ with probability $0.4$ or moves to $M$ with probability $0.6$. From $M$ he stays at $M$ with probability $0.5$, moves to $H$ with probability $0.3$, or to $L$ with probability $0.2$. From $H$ he stays at $H$ with probability $0.3$ or moves to $M$ with probability $0.7$.

Construct the transition matrix $P$ in the order ($L,M,H$).

For the transition matrix
$$P=\left(\begin{array}{ccc}0.2& 0.5& 0.3\\ 0.1& 0.6& 0.3\\ 0.4& 0.4& 0.2\end{array}\right),$$

what is the probability that the chain moves from state C (3) to state B (2) in one step?

A customer moves among four shops $A$, $B$, $C$, and $D$.

From $A$, they stay in $A$ with probability $0.1$, go to $B$ with $0.4$, $C$ with $0.3$, and $D$ with $0.2$. From $B$, they stay in $B$ with probability $0.2$, go to $A$ with $0.2$, $C$ with $0.5$, and $D$ with $0.1$. From $C$, they stay in $C$ with probability $0$, go to $A$ with $0.3$, $B$ with $0.3$, and $D$ with $0.4$. From $D$, they stay in $D$ with probability $0.25$, go to $A$ with $0.25$, $B$ with $0.25$, and $C$ with $0.25$.

Construct the transition matrix $P$ for this customer's movement in the order $(A,B,C,D)$.

Verify that the matrix $$P=\left(\begin{array}{ccc}0.5& 0.3& 0.2\\ 0.4& 0.4& 0.2\\ 0.2& 0.5& 0.3\end{array}\right)$$ is a valid transition matrix.