Exercises for Question Type 4: Finding the shortest path in weighted graphs using Dijkstra's Algorithm

Loading subject…

Exercises for Question Type 4: Finding the shortest path in weighted graphs using Dijkstra's Algorithm - IB

Question 1

Apply the Floyd-Warshall algorithm to detect whether there is a negative-weight cycle in the graph represented by the matrix W = 0 \infty \infty - 5 40 \infty \infty \infty - 2 0 \infty \infty \infty - 1 0 and state your conclusion.

[4]

Question 2

Consider the directed graph with vertices v_{0}, v_{1}, v_{2}, v_{3} and weighted edges (v_{0} \to v_{1} : 5), (v_{0} \to v_{2} : 3), (v_{1} \to v_{2} : 2), (v_{1} \to v_{3} : 6), (v_{2} \to v_{3} : 7) . Use Dijkstra’s algorithm to determine the shortest path from v_{0} to v_{3} .

[5]

Question 3

Given a weighted directed graph with vertices 1-5 and weight matrix W : W = 03 \infty 7 \infty 301 \infty 4 \infty 1025 7 \infty 206 \infty 4560 Use the Floyd-Warshall algorithm to determine the shortest distances between all pairs of vertices. Show the updates for each iteration k = 1, 2, 3, 4, 5 .

[5]

Question 4

Consider the weighted directed graph with vertices {1, 2, 3, 4} and edges: 1 \to 2 with weight 3, 2 \to 3 with weight 4, 3 \to 4 with weight - 10, and 4 \to 2 with weight 2 . Use the Floyd-Warshall algorithm to determine whether this graph contains a negative cycle and compute the shortest-path distances if possible.

[5]

Question 5

Floyd-Warshall algorithm for finding shortest paths in a weighted graph.

Apply the Floyd-Warshall algorithm to the following weight matrix W for vertices {X, Y, Z} : W = 0 \infty \infty 20 \infty 810 State the final distance matrix.

[3]

Question 6

Apply Dijkstra's algorithm to find shortest paths in a weighted graph.

Apply Dijkstra’s algorithm to a weighted undirected graph with vertices {1, 2, 3, 4, 5} and the following edges: {1, 2} with weight 2 {1, 3} with weight 4 {2, 3} with weight 1 {2, 4} with weight 7 {3, 5} with weight 3 {4, 5} with weight 1 Determine the order in which vertices are selected and the final shortest distances from vertex 1 to all other vertices.

[6]

Question 7

Given the adjacency matrix of a directed graph with vertices {1, 2, 3, 4}, using \infty for no direct edge: W = 0852 30 \infty \infty \infty 20 \infty 7 \infty 10 Apply the Floyd-Warshall algorithm to compute the final distance matrix.

[6]

Question 8

Using Dijkstra’s algorithm, find the shortest path from node 1 to node 6 in the weighted graph with the following edges: 1 - 2 : 7, 1 - 3 : 9, 1 - 6 : 14, 2 - 3 : 10, 2 - 4 : 15, 3 - 4 : 11, 3 - 6 : 2, 4 - 5 : 6, 5 - 6 : 9 State the shortest distance and the actual path.

[5]

Question 9

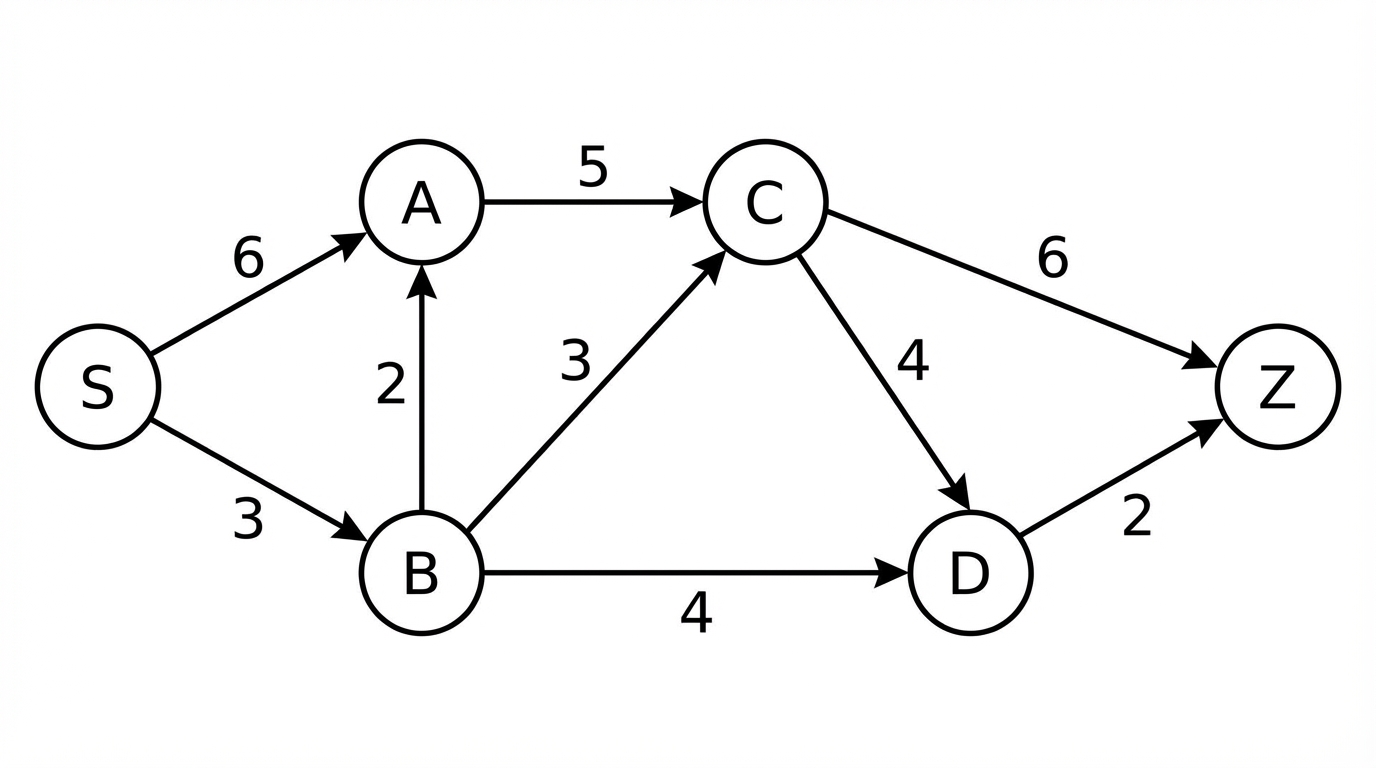
Use Dijkstra’s algorithm, starting at node S, to find the shortest path to node Z in the graph shown below. Draw on this The edges and their respective weights are: S - A : 6, S - B : 3, A - C : 5, B - A : 2, B - C : 3, C - D : 4, D - Z : 2, C - Z : 6 . Determine the shortest path and its total weight.

[5]

Question 10

Use the Floyd-Warshall algorithm on the directed graph with weight matrix W = 0 \infty \infty \infty \infty 10 \infty \infty \infty \infty 20 \infty \infty 4 \infty 30 \infty \infty \infty 510 to find the length of the shortest path from vertex 1 to vertex 5. Show all iterations that change the shortest path estimate from vertex 1 to vertex 5.

[4]

Question 11

A weighted graph has vertices {A, B, C, D, E} . The weight matrix W for the graph is given by: W = 075 \infty \infty 70386 5304 \infty \infty 8402 \infty 6 \infty 20 Use the Floyd-Warshall algorithm to find the shortest distance between vertex B and vertex E . Show your working for each iteration of the intermediate vertices.

[6]

Question 12

The following weighted undirected graph has vertices A, B, C, D, E and edge weights: A B = 4, A C = 2, B C = 1, B D = 5, C D = 8, C E = 10, D E = 2 .

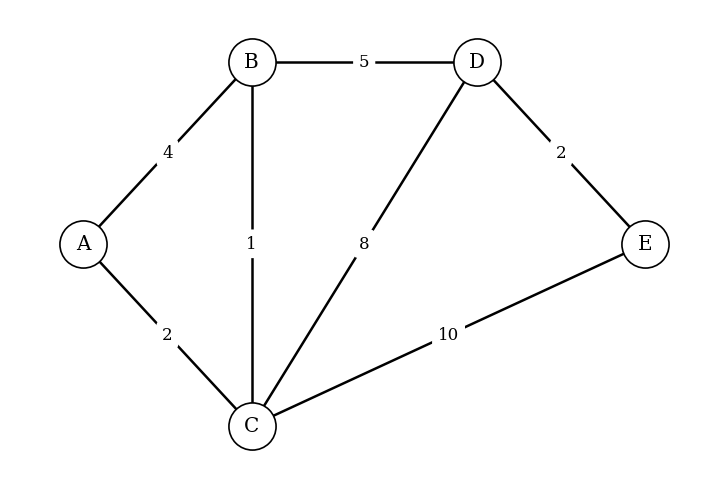
Apply Dijkstra’s algorithm to the graph to find the shortest path distances from vertex A to all other vertices. Show your working clearly.

[6]

IB Mathematics Applications & Interpretation Question Type 4: Finding the Shortest Path in Weighted Graphs Using Dijkstra's Algorithm Exercises