Emission Line Spectra of Hydrogen and Energy Transitions
The Emission Line Spectrum of Hydrogen: Evidence for Discrete Energy Levels
- When a pure gaseous element like hydrogen is subjected to high voltage under reduced pressure, it emits light.
- Passing this light through a prism produces a line emission spectrum, a series of distinct lines, each corresponding to a specific wavelength of light.
- Unlike a continuous spectrum, which includes all wavelengths (like a rainbow), the line spectrum has clear gaps. But why do these gaps occur?
Quantization of Energy Levels
- The hydrogen line spectrum arises because electrons in hydrogen atoms can only occupy specific, discrete energy levels.
- When an electron absorbs energy, it "jumps" to a higher energy level (excited state).
- When it falls back to a lower energy level, it releases energy in the form of a photon.
- The energy of this photon corresponds precisely to the difference between the two energy levels.
- Mathematically, the energy of an electron in a hydrogen atom is described by the equation: $$E_n = -R_H \frac{1}{n^2} $$ where:
- $E_n$ = energy of the electron in the $n$-th energy level (in joules, $\text{J}$)
- $R_H = 2.18 \times 10^{-18} \, \text{J}$ (Rydberg constant)
- $n$ = principal quantum number (1, 2, 3, ...)
The negative sign indicates that the energy is relative to the ionized state, where the electron is completely removed from the atom ($n = \infty$).
- Think of the energy levels like steps on a staircase.
- You can stand on any step, but you can’t hover between them.
- Similarly, electrons can only "stand" on specific energy levels.
Convergence of Lines at Higher Energies
- If you examine the hydrogen spectrum closely, you’ll notice that the lines become closer together (converge) at higher energy levels.
- This convergence occurs because the energy levels themselves get closer as $n$ increases.
- At the limit of convergence, the energy difference between levels approaches zero, corresponding to the ionization of the atom.
Energy Transitions: Linking Energy Levels to Spectral Lines
- Each line in the hydrogen spectrum corresponds to an electron transitioning between two energy levels.
- The energy of the emitted photon is directly related to the difference in energy between these levels: $$\Delta E = E_{\text{higher}} - E_{\text{lower}}$$
- Using Planck’s equation, the energy of the photon can also be expressed as: $$E = h \cdot f = \frac{h \cdot c}{\lambda}$$ where:
- $h = 6.63 \times 10^{-34} \, \text{J s}$ (Planck’s constant)
- $f$ = frequency of the photon (in $\text{Hz}$)
- $c = 3.00 \times 10^8 \, \text{m s}^{-1}$ (speed of light)
- $\lambda$ = wavelength of the photon (in meters)
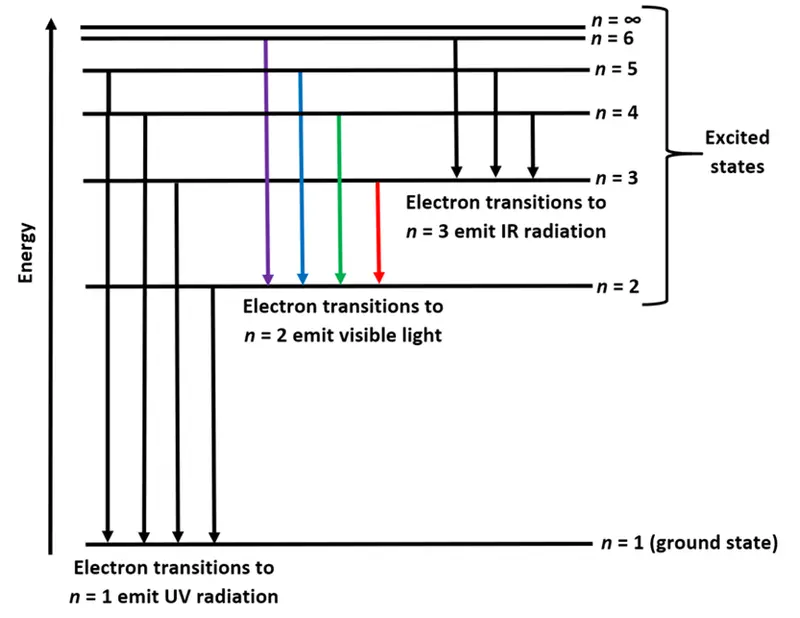
The Balmer, Lyman, and Paschen Series
The hydrogen spectrum is divided into series based on the final energy level ($n_f$) to which the electron transitions:
- Lyman Series: Transitions to $n_f = 1$ (UV region)
- Balmer Series: Transitions to $n_f = 2$ (visible region)
- Paschen Series: Transitions to $n_f = 3$ (infrared region)
In IB Chemistry (First Examination 2025) you are not required to know the names of the series by heart.
- The red line in the Balmer series corresponds to an electron falling from $n = 3$ to $n = 2$, emitting a photon with a wavelength of 656 nm.
- The violet line corresponds to a transition from $n = 6$ to $n = 2$, with a shorter wavelength of 410 nm.
Calculate the wavelength of light emitted when an electron in a hydrogen atom transitions from $n = 4$ to $n = 2$.
Solution
- Using the energy formula for hydrogen:
$$
E_n = -R_H \frac{1}{n^2}
$$ - Energy at $n = 4$:$$
E_4 = -2.18 \times 10^{-18} \frac{1}{4^2} = -1.36 \times 10^{-19} \, \text{J}
$$ - Energy at $n = 2$:$$
E_2 = -2.18 \times 10^{-18} \frac{1}{2^2} = -5.45 \times 10^{-19} \, \text{J}
$$ - Calculate the energy difference:
$$
\Delta E = E_2 - E_4 = -5.45 \times 10^{-19} - (-1.36 \times 10^{-19}) = 4.09 \times 10^{-19} \, \text{J}
$$ - Use Planck’s equation to find the wavelength:
$$
\lambda = \frac{h \cdot c}{\Delta E}
$$ - Substituting values:
$$
\lambda = \frac{6.63 \times 10^{-34} \cdot 3.00 \times 10^8}{4.09 \times 10^{-19}} = 486 \, \text{nm}
$$ - This corresponds to the cyan line in the Balmer series.
- Students often forget to convert units when solving problems involving energy and wavelength.
- Always ensure that energy is in joules (J), wavelength in meters (m), and frequency in hertz (Hz).
- Why do the lines in the hydrogen spectrum converge at higher energies?
- If an electron transitions from $n = 5$ to $n = 3$, in which region of the electromagnetic spectrum would the emitted photon lie?
- How does the energy difference between levels change as $n$ increases?