R3.1.13 pH curves of Acid-Base combinations (Higher Level Only) Notes

General Shapes of pH Curves

1. You are conducting a titration experiment, carefully adding a base to an acid (or vice versa).
2. Each drop of titrant tells part of a story, and when you plot the pH against the volume of titrant added, you reveal the full narrative: a pH curve.

Key Features of pH Curves

Before diving into specific examples, let’s define the key features of a pH curve:

1. Intercept with the pH axis:
   1. This represents the initial pH of the solution, determined by the strength and concentration of the analyte (the substance being titrated).
2. Equivalence point:
   1. The point where the moles of acid equal the moles of base added.
   2. The pH at this point depends on the strength of the acid and base.
3. Buffer region:
   1. A relatively flat section of the curve, observed in titrations involving weak acids or bases, where the solution resists changes in pH.
4. Points where $ \text{pH} = \text{pKa} $ or $ \text{pOH} = \text{pKb} $:
   1. These occur halfway to the equivalence point in weak acid-base titrations and are critical for identifying the acid/base strength.

Strong Acid + Strong Base

1. The curve starts at a low initial pH(around 1 or lower for a 0.1 M strong acid) because strong acids like HCl or HNO(_3) fully dissociate, producing a high concentration of $ \text{H}^+ $ ions.
2. The pH rises gradually at first, then increases sharply near the equivalence point.
3. At the equivalence point, the pH is exactly 7, as the neutralization produces only water and a neutral salt (e.g., NaCl from HCl and NaOH).
4. After the equivalence point, the pH levels off at a high value(around 13–14) due to the excess strong base.

Weak Base + Strong Acid

1. The curve begins at a high initial pH because the weak base (e.g., ammonia, $NH_3$) only partially ionizes, producing a low concentration of hydroxide ions $OH^-$.
2. As the strong acid is added, the pH drops gradually since the weak base reacts incompletely with the $H^+$ ions, forming its conjugate acid (e.g., $NH_4^+$).
3. The equivalence point occurs at a pH less than 7 because the conjugate acid formed (e.g., $NH_4^+$) hydrolyzes, releasing additional $H^+$ ions, making the solution slightly acidic.
4. Beyond the equivalence point, the pH decreases sharply as excess strong acid dominates the solution, contributing a high concentration of free $H^+$ ions.

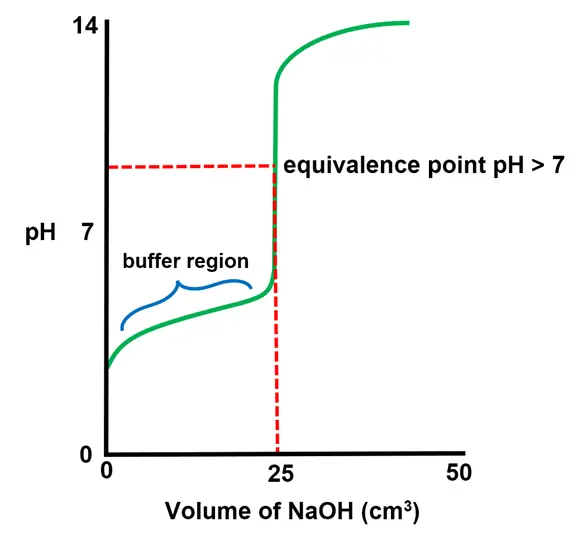
Weak Acid + Strong Base

1. The curve starts at a higher initial pH (around 3–5) compared to strong acids, as weak acids (e.g., $CH_3COOH$ only partially dissociate.
2. A buffer region appears before the equivalence point, where the solution contains both the weak acid and its conjugate base. In this region, the pH changes slowly despite the addition of the base.
3. At the half-equivalence point, $ \text{pH} = \text{pKa} $, as the concentrations of the weak acid and its conjugate base are equal.
4. The equivalence point occurs at a pH greater than 7, as the conjugate base of the weak acid (e.g., $CH_3COO^-$ hydrolyzes to produce $ \text{OH}^- $ ions.
5. After the equivalence point, the pH levels off at a high value due to the excess strong base.

Weak Acid + Weak Base

1. The curve starts at a moderate initial pH (around 3–5), depending on the strength of the weak acid.
2. A buffer region appears before the equivalence point, similar to the weak acid + strong base case.
3. The equivalence point occurs at a pH close to 7, as both the conjugate acid and base hydrolyze, partially neutralizing each other.
4. The pH change near the equivalence point is much less sharp, making it difficult to identify the equivalence point accurately.
5. Beyond the equivalence point, the pH levels off gradually.

Experimental Considerations

When performing titrations to generate pH curves, it’s important to ensure accuracy:

1. Smaller increments near the equivalence point: Add smaller volumes of titrant as you approach the equivalence point, as the pH changes rapidly in this region.
2. Calibrate pH meters: Use standard buffer solutions to calibrate your pH meter before starting the experiment.
3. Stir thoroughly: Ensure the solution is well-mixed after each addition of titrant to avoid localized pH variations.