R1.4.4 Gibbs free energy and equilibrium (Higher Level Only) Notes

Gibbs Free Energy, Equilibrium, and Spontaneity

$ΔG$ and Reaction Progress

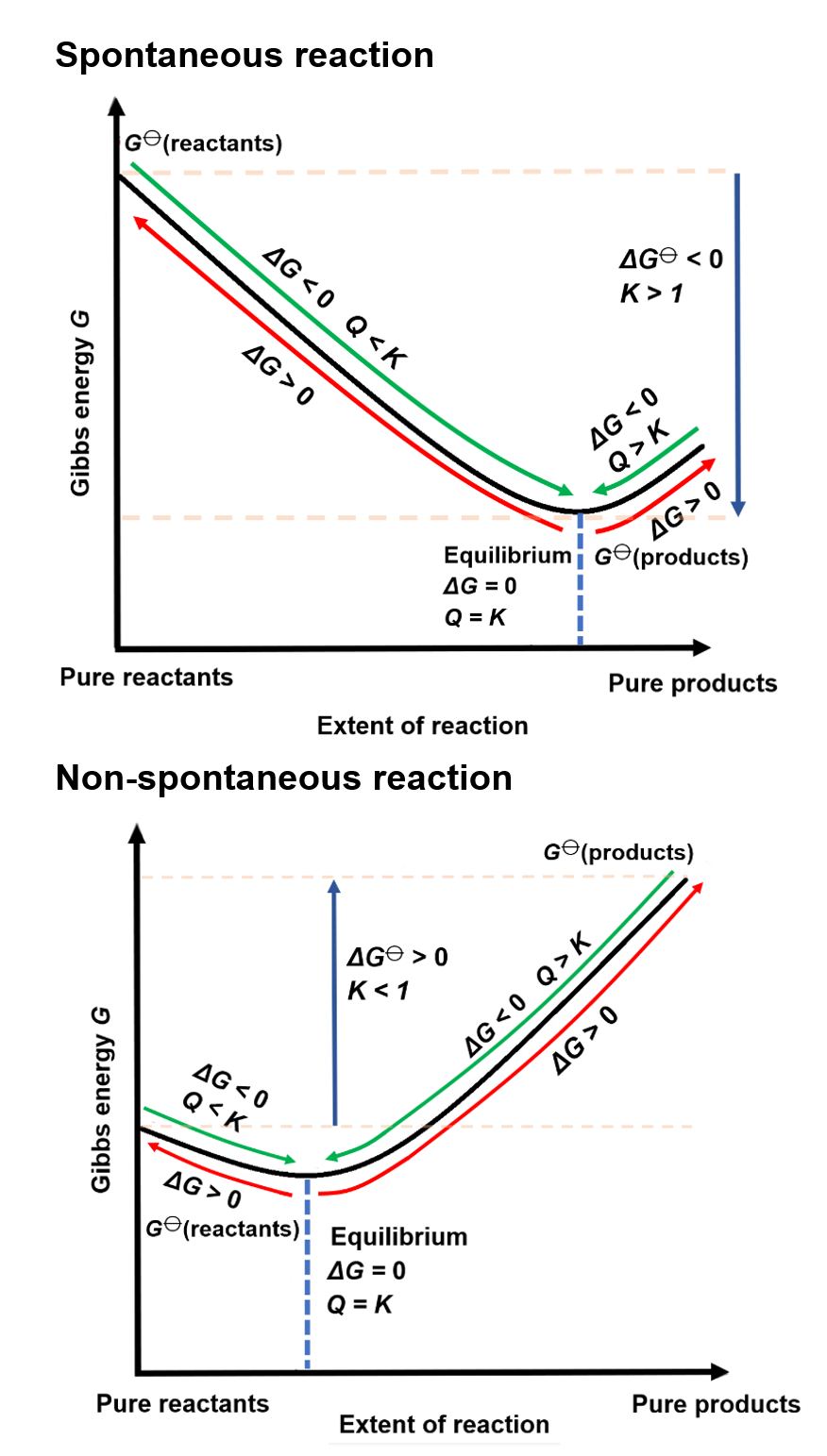
1. As discussed in the previous sections, Gibbs free energy ($ \Delta G $) is a thermodynamic quantity that helps us predict whether a reaction is spontaneous under constant pressure and temperature.
2. A reaction is spontaneous if $ \Delta G $ is negative, meaning it can proceed without external energy input.
3. However, as a reaction progresses, the concentrations of reactants and products change, and so does $ \Delta G $.
4. At the start of a reaction, $ \Delta G $ is often negative, favoring the forward reaction.
5. As the reaction progresses, $ \Delta G $ becomes less negative as the system approaches equilibrium.
6. At equilibrium, $ \Delta G = 0 $. At this point, there is no net change in the concentrations of reactants and products because the forward and reverse reactions occur at the same rate.

The Relationship Between ΔG and the Equilibrium Constant (K)

1. At equilibrium, the concentrations of products and reactants form a constant ratio, defined as the equilibrium constant ($ K $).
2. The relationship between $ \Delta G $ and $ K $ is expressed by the equation: $$ \Delta G^\circ = -RT \ln K $$ where:
   1. $ \Delta G^\circ $: Standard Gibbs free energy change ($kJ \, mol^{-1}$) under standard conditions.
   2. $ R $: Gas constant ($ 8.31 \, \text{J mol}^{-1} \, \text{K}^{-1} $).
   3. $ T $: Temperature in Kelvin (K).
   4. $ K $: Equilibrium constant (unitless).

This equation links the thermodynamic favorability of a reaction (as indicated by $ \Delta G^\circ $) to the position of equilibrium (as characterized by $ K $).

Key Insights:

1. If $ \Delta G^\circ < 0$:
   1. The reaction favors products at equilibrium ($ K > 0$)
2. If $ \Delta G^\circ > 0 $:
   1. The reaction favors reactants at equilibrium ($ K <0$)
3. If $\Delta G^\circ = 0 $:
   1. Neither reactants nor products are favored ($ K = 1 $).

Predicting Equilibrium Composition

The sign and magnitude of $ \Delta G^\circ $ provide valuable insights into the equilibrium composition of a reaction mixture:

1. If $ \Delta G^\circ <0$:
   1. The products are more stable than the reactants, so the equilibrium mixture will be product-rich.
2. If $\Delta G^\circ > 0$:
   1. The reactants are more stable than the products, so the equilibrium mixture will be reactant-rich.

The Relationship Between $ΔG$ and the Reaction Quotient ($Q$)

1. The equation:
2. $$\Delta G = \Delta G^\circ + RT \ln Q$$ relates the Gibbs free energy change ($\Delta G$) of a reaction under non-standard conditions to its standard Gibbs free energy change ($\Delta G^\circ$) and the reaction quotient ($Q$).
3. When $Q$ differs from the equilibrium constant ($K$), the system is not at equilibrium, and the sign of $\Delta G$ determines whether the reaction will shift towards products or reactants to reach equilibrium.

Key Insights from the Equation:

1. If $Q < K$: $\Delta G < 0$, the reaction is spontaneous in the forward direction as the system moves toward equilibrium.
2. If $Q > K$: $\Delta G > 0$, the reaction is non-spontaneous in the forward direction and will shift towards reactants.
3. If $Q = K$: $\Delta G = 0$, the system is at equilibrium with no net change in reactant or product concentrations.